|
 |
The polynomial object (and its "shortcut" versions: cubic,
quartic and quadric)
of POV-Ray is one of the most complex and mathematical primitives of the program. One could think that it is seldom
used and more or less obsolete, but we have to remember that for example the torus primitive is just a shortcut for
the equivalent quartic, which is just a shortcut for the equivalent poly object. Polys are,
however, seldom used in scenes due to the fact that they are so difficult to define and it is far from trivial to get
the desired shape with just a polynomial equation. It is mostly used by the most mathematically oriented POV-Ray
users.
This tutorial explains the process of making a polynomial object in POV-Ray.
Note:Since version 3.5, POV-Ray includes the new isosurface object which
makes the polynomial object more or less obsolete. The isosurface is more versatile (you can specify any mathematical
function, not just polynomials), easier to use. You can write the function as is, without needing to put values in a
gigantic vector. Isosurfaces often render considerably faster than equivalent polys.
However, the most mathematically oriented still like polys because isosurfaces are calculated just by approximating
the right value, while the poly is calculated in a mathematically exact way. Usually isosurfaces are more than good
enough for most applications, though.
Note: at maximum a 15th degree polynomial can be represented with the poly object. If
a higher degree polynomial or other non-polynomial function has to be represented, then it is necessary to use the
isosurface object.
1.3.3.4.1 Creating the polynomial function
The first step is to create the polynomial function to be represented. You will need some (high-school level)
mathematical knowledge for this.
1) Let's start with an easy example: A sphere.
The sphere function is:
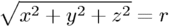
Now we have to convert this to polynomial form:
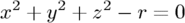
We will need a polynomial of the 2nd degree to represent this.
2) A more elaborated example:
Let's take the function:
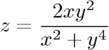
Converting this to polynomial form we get:
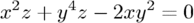
Although the highest power is 4 we will need a 5th order polynomial to represent this function (because we cannot
represent y4z with a 4th order polynomial).
3) And since we talked about the torus, let's also take it as an example.
A torus can be represented with the function:
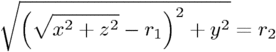
where r1 is the major radius and r2 is the minor radius.
Now, this is tougher to convert to polynomial form, but finally we get:
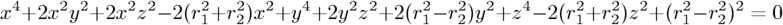
A 4th order polynomial is enough to represent this.
Note: not every function can be represented in polynomial form. Only functions that
use addition (and substraction), multiplication (and division) and scalar powers (including rational powers, eg. the
square root) can be represented. Also, the poly primitive supports only polynomials of the 7th degree at max.
Converting a function to polynomial form may be a very laborious task for certain functions. Some mathematical
programs are very helpful in this matter.
1.3.3.4.2 Writing the polynomial vector
Now that we have the function in polynomial form, we have to write it in POV-Ray syntax. The syntax is specified in
the in the chapters "Poly, Cubic and Quartic" and "Quadric"
of the SDL section. There is also a table in this chapter which we will be using to make the polynomial vector. It is
easier to have this table printed on paper.
Note: It is also possible to make a little program with your favorite programming
language which will print the poly vector from the polynomial function, but making a program like this is up to you.
1) Let's start with the easy one, ie. the sphere.
Since the sphere can be represented with a polynomial of 2nd degree, we look at the row titled "2nd" in
the table. We see that it has 10 items, ie. we need a vector of size 10. Each item of the vector will be the factor of
the term listed in the table.
The polynomial was:
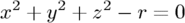
Writing the poly in this way we get:
#declare Radius=1;
poly
{ 2,
<1,0,0,0,1,
0,0,1,0,-Radius*Radius>
}
Put each group of factors (separated with lines in the table) in their own lines.
In the table we see that the first item is the factor for x2, which is 1 in the function. The next item
is xy. Since it is not in the function, its factor is 0. Likewise the next item, which is xz. And so on. The last item
is the scalar term, which is in this case -r2.
If we make a proper scene and render it, we get:
camera { location y*4-z*5 look_at 0 angle 35 }
light_source { <100,200,-50> 1 }
background { rgb <0,.25,.5> }
#declare Radius=1;
poly
{ 2,
<1,0,0,0,1,
0,0,1,0,-Radius*Radius>
pigment { rgb <1,.7,.3> } finish { specular .5 }
}

Note: there is a shortcut for 2nd degree polynomials: The quadric
primitive. Using a shortcut version, whenever possible, can lead to faster renderings. We can write the sphere code
described above in the following way:
quadric
{ <1,1,1>, <0,0,0>, <0,0,0>, -Radius*Radius
pigment { rgb <1,.7,.3> } finish { specular .5 }
}
2) Now lets try the second one. We do it similarly, but this time we need to look at the row
titled "5th" in the table.
The polynomial was:
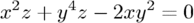
Writing the poly primitive we get:
poly
{ 5,
<0,0,0,0,0,
0,0,0,0,0,
0,0,0,0,0,
0,0,0,1,0,
0,0,0,0,0,
-2,0,0,0,0,
0,0,0,0,0,
0,1,0,0,0,
0,0,0,0,0,
0,0,0,0,0,
0,0,0,0,0,0>
}
With the proper scene we get:
camera { location <8,20,-10>*.7 look_at x*.01 angle 35 }
light_source { <100,200,20> 1 }
background { rgb <0,.25,.5> }
poly
{ 5,
<0,0,0,0,0,
0,0,0,0,0,
0,0,0,0,0,
0,0,0,1,0,
0,0,0,0,0,
-2,0,0,0,0,
0,0,0,0,0,
0,1,0,0,0,
0,0,0,0,0,
0,0,0,0,0,
0,0,0,0,0,0>
clipped_by { box { <-4,-4,-1><4,4,1> } }
bounded_by { clipped_by }
pigment { rgb <1,.7,.3> } finish { specular .5 }
rotate <0,90,-90>
}

3) And finally the torus:
The polynomial was:
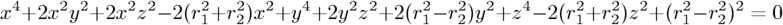
And we get the proper 4th degree poly primitive:
camera { location y*4-z*5 look_at 0 angle 35 }
light_source { <100,200,-50> 1 }
background { rgb <0,.25,.5> }
#declare r1=1;
#declare r2=.5;
poly
{ 4,
<1,0,0,0,2,
0,0,2,0,-2*(r1*r1+r2*r2),
0,0,0,0,0,
0,0,0,0,0,
1,0,0,2,0,
2*(r1*r1-r2*r2),0,0,0,0,
1,0,-2*(r1*r1+r2*r2),0,pow(r1,4)+pow(r2,4)-2*r1*r1*r2*r2>
pigment { rgb <1,.7,.3> } finish { specular .5 }
}
When rendered we get:

There is a shortcut for 4th order polynomials: The quartic
primitive. We can write the torus like this:
quartic
{ <1,0,0,0,2,
0,0,2,0,-2*(r1*r1+r2*r2),
0,0,0,0,0,
0,0,0,0,0,
1,0,0,2,0,
2*(r1*r1-r2*r2),0,0,0,0,
1,0,-2*(r1*r1+r2*r2),0,pow(r1,4)+pow(r2,4)-2*r1*r1*r2*r2>
pigment { rgb <1,.7,.3> } finish { specular .5 }
}
|
 |






