|
 |
In the real world, lathe refers to a process of making
patterned rounded shapes by spinning the source material in place and carving pieces out as it turns. The results can
be elaborate, smoothly rounded, elegant looking artefacts such as table legs, pottery, etc. In POV-Ray, a lathe object
is used for creating much the same kind of items, although we are referring to the object itself rather than the means
of production.
Here is some source for a really basic lathe.
#include "colors.inc"
background{White}
camera {
angle 10
location <1, 9, -50>
look_at <0, 2, 0>
}
light_source {
<20, 20, -20> color White
}
lathe {
linear_spline
6,
<0,0>, <1,1>, <3,2>, <2,3>, <2,4>, <0,4>
pigment { Blue }
finish {
ambient .3
phong .75
}
}

We render this, and what we see is a fairly simply type of lathe, which looks like a child's top. Let's take a look
at how this code produced the effect.
First, a set of six points is declared which the raytracer connects with lines. We note that there are only two
components in the vectors which describe these points. The lines that are drawn are assumed to be in the x-y-plane,
therefore it is as if all the z-components were assumed to be zero. The use of a two-dimensional vector is mandatory
(Attempting to use a 3D vector would trigger an error... with one exception, which we will explore later in the
discussion of splines).
Once the lines are determined, the ray-tracer rotates this line around the y-axis, and we can imagine a trail being
left through space as it goes, with the surface of that trail being the surface of our object.
The specified points are connected with straight lines because we used the linear_spline keyword.
There are other types of splines available with the lathe, which will result in smooth curving lines, and even rounded
curving points of transition, but we will get back to that in a moment.
First, we would like to digress a moment to talk about the difference between a lathe and a surface of revolution
object (SOR). The SOR object, described in a separate tutorial, may seem terribly similar to the lathe at first
glance. It too declares a series of points and connects them with curving lines and then rotates them around the
y-axis. The lathe has certain advantages, such as different kinds of splines, linear, quadratic and cubic, and one
more thing:
The simpler mathematics used by a SOR does not allow the curve to double back over the same y-coordinates, thus, if
using a SOR, any sudden twist which cuts back down over the same heights that the curve previously covered will
trigger an error. For example, suppose we wanted a lathe to arc up from <0,0> to <2,2>, then to dip back
down to <4,0>. Rotated around the y-axis, this would produce something like a gelatin mold - a rounded semi
torus, hollow in the middle. But with the SOR, as soon as the curve doubled back on itself in the y-direction, it
would become an illegal declaration.
Still, the SOR has one powerful strong point: because it uses simpler order mathematics, it generally tends to
render faster than an equivalent lathe. So in the end, it is a matter of: we use a SOR if its limitations will allow,
but when we need a more flexible shape, we go with the lathe instead.
1.3.1.1.1 Understanding The Concept of Splines
It would be helpful, in order to understand splines, if we had a sort of Spline Workshop where we could
practice manipulating types and points of splines and see what the effects were like. So let's make one! Now that we
know how to create a basic lathe, it will be easy:
#include "colors.inc"
camera {
orthographic
up <0, 5, 0>
right <5, 0, 0>
location <2.5, 2.5, -100>
look_at <2.5, 2.5, 0>
}
/* set the control points to be used */
#declare Red_Point = <1.00, 0.00>;
#declare Orange_Point = <1.75, 1.00>;
#declare Yellow_Point = <2.50, 2.00>;
#declare Green_Point = <2.00, 3.00>;
#declare Blue_Point = <1.50, 4.00>;
/* make the control points visible */
cylinder { Red_Point, Red_Point - <0,0,20>, .1
pigment { Red }
finish { ambient 1 }
}
cylinder { Orange_Point, Orange_Point - <0,0,20>, .1
pigment { Orange }
finish { ambient 1 }
}
cylinder { Yellow_Point, Yellow_Point - <0,0,20>, .1
pigment { Yellow }
finish { ambient 1 }
}
cylinder { Green_Point, Green_Point - <0,0,20>, .1
pigment { Green }
finish { ambient 1 }
}
cylinder { Blue_Point, Blue_Point- <0,0,20>, .1
pigment { Blue }
finish { ambient 1 }
}
/* something to make the curve show up */
lathe {
linear_spline
5,
Red_Point,
Orange_Point,
Yellow_Point,
Green_Point,
Blue_Point
pigment { White }
finish { ambient 1 }
}
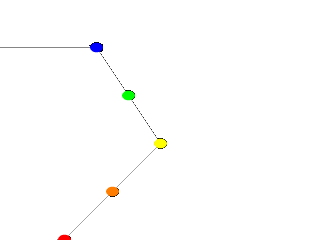
Now, we take a deep breath. We know that all looks a bit weird, but with some simple explanations, we can easily
see what all this does.
First, we are using the orthographic camera. If we have not read up on that yet, a quick summary is: it renders the
scene flat, eliminating perspective distortion so that in a side view, the objects look like they were drawn
on a piece of graph paper (like in the side view of a modeler or CAD package). There are several uses for this
practical new type of camera, but here it is allowing us to see our lathe and cylinders edge on, so that what
we see is almost like a cross section of the curve which makes the lathe, rather than the lathe itself. To further
that effect, we eliminated shadowing with the ambient 1 finish, which of course also eliminates the need
for lighting. We have also positioned this particular side view so that <0,0> appears at the lower left of our
scene.
Next, we declared a set of points. We note that we used 3D vectors for these points rather than the 2D vectors we
expect in a lathe. That is the exception we mentioned earlier. When we declare a 3D point, then use it in a lathe, the
lathe only uses the first two components of the vector, and whatever is in the third component is simply ignored. This
is handy here, since it makes this example possible.
Next we do two things with the declared points. First we use them to place small diameter cylinders at the
locations of the points with the circular caps facing the camera. Then we re-use those same vectors to determine the
lathe.
Since trying to declare a 2D vector can have some odd results, and is not really what our cylinder declarations
need anyway, we can take advantage of the lathe's tendency to ignore the third component by just setting the
z-coordinate in these 3D vectors to zero.
The end result is: when we render this code, we see a white lathe against a black background showing us how the
curve we have declared looks, and the circular ends of the cylinders show us where along the x-y-plane our control
points are. In this case, it is very simple. The linear spline has been used so our curve is just straight lines
zig-zagging between the points. We change the declarations of Red_Point and Blue_Point to
read as follows.
#declare Red_Point = <2.00, 0.00>;
#declare Blue_Point = <0.00, 4.00>;
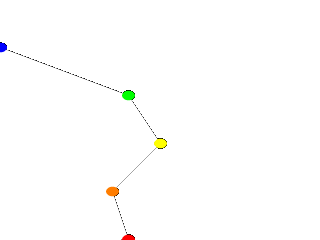
We re-render and, as we can see, all that happens is that the straight line segments just move to accommodate the
new position of the red and blue points. Linear splines are so simple, we could manipulate them in our sleep, no?
Let's try something different. First, we change the points to the following.
#declare Red_Point = <1.00, 0.00>;
#declare Orange_Point = <2.00, 1.00>;
#declare Yellow_Point = <3.50, 2.00>;
#declare Green_Point = <2.00, 3.00>;
#declare Blue_Point = <1.50, 4.00>;
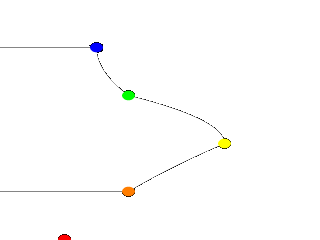
We then go down to the lathe declaration and change linear_spline to quadratic_spline. We
re-render and what do we have? Well, there is a couple of things worthy of note this time. First, we will see that
instead of straight lines we have smooth arcs connecting the points. These arcs are made from quadratic curves, so our
lathe looks much more interesting this time. Also, Red_Point is no longer connected to the curve. What
happened?
Well, while any two points can determine a straight line, it takes three to determine a quadratic curve. POV-Ray
looks not only to the two points to be connected, but to the point immediately preceding them to determine the formula
of the quadratic curve that will be used to connect them. The problem comes in at the beginning of the curve. Beyond
the first point in the curve there is no previous point. So we need to declare one. Therefore, when using a
quadratic spline, we must remember that the first point we specify is only there so that POV-Ray can determine what
curve to connect the first two points with. It will not show up as part of the actual curve.
There is just one more thing about this lathe example. Even though our curve is now put together with smooth
curving lines, the transitions between those lines is... well, kind of choppy, no? This curve looks like the lines
between each individual point have been terribly mismatched. Depending on what we are trying to make, this could be
acceptable, or, we might long for a more smoothly curving shape. Fortunately, if the latter is true, we have another
option.
The quadratic spline takes longer to render than a linear spline. The math is more complex. Taking longer still is
the cubic spline, yet for a really smoothed out shape this is the only way to go. We go back into our example, and
simply replace quadratic_spline with cubic_spline. We render one more time, and take a look
at what we have.
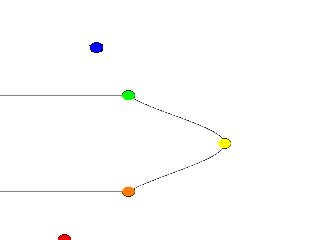
While a quadratic spline takes three points to determine the curve, a cubic needs four. So, as we might expect, Blue_Point
has now dropped out of the curve, just as Red_Point did, as the first and last points of our curve are
now only control points for shaping the curves between the remaining points. But look at the transition from
Orange_Point to Yellow_Point and then back to Green_Point. Now, rather than looking
mismatched, our curve segments look like one smoothly joined curve.
finally there is another kind of quadratic spline, the bezier_spline. This one takes four points per
section. The start point, the end points and in between, two control points. To use it, we will have to make a few
changes to our work shop. Delete the Yellow point, delete the Yellow cylinder. Change the points to:
#declare Red_Point = <2.00, 1.00>;
#declare Orange_Point = <3.00, 1.50>;
#declare Green_Point = <3.00, 3.50>;
#declare Blue_Point = <2.00, 4.00>;
And change the lathe to:
lathe {
bezier_spline
4,
Red_Point,
Orange_Point,
Green_Point,
Blue_Point
pigment { White }
finish { ambient 1 }
}
The, green and orange, control points are not connected to the curve. Move them around a bit, for example #declare
Orange_Point = <1.00, 1.50>;. The line that can be drawn from the start point to its closest control
point (red to orange) shows the tangent of the curve at the start point. Same for the end point, blue to green.
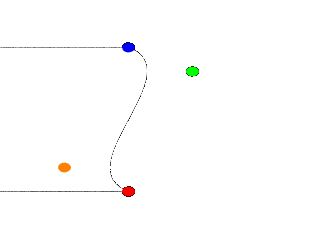
One spline segment is nice, two is nicer. So we will add another segment and connect it to the blue point. One
segment has four points, so two segments have eight. The first point of the second segment is the same as the last
point of the first segment. The blue point. So we only have to declare three more points. Also we have to move the
camera a bit and add more cylinders. Here is the complete scene again:
#include "colors.inc"
camera {
orthographic
up <0, 7, 0>
right <7, 0, 0>
location <3.5, 4, -100>
look_at <3.5, 4, 0>
}
/* set the control points to be used */
#declare Red_Point = <2.00, 1.00>;
#declare Orange_Point = <1.00, 1.50>;
#declare Green_Point = <3.00, 3.50>;
#declare Blue_Point = <2.00, 4.00>;
#declare Green_Point2 = <3.00, 4.50>;
#declare Orange_Point2= <1.00, 6.50>;
#declare Red_Point2 = <2.00, 7.00>;
/* make the control points visible */
cylinder { Red_Point, Red_Point - <0,0,20>, .1
pigment { Red } finish { ambient 1 }
}
cylinder { Orange_Point, Orange_Point - <0,0,20>, .1
pigment { Orange } finish { ambient 1 }
}
cylinder { Green_Point, Green_Point - <0,0,20>, .1
pigment { Green } finish { ambient 1 }
}
cylinder { Blue_Point, Blue_Point- <0,0,20>, .1
pigment { Blue } finish { ambient 1 }
}
cylinder { Green_Point2, Green_Point2 - <0,0,20>, .1
pigment { Green } finish { ambient 1 }
}
cylinder { Orange_Point2, Orange_Point2 - <0,0,20>, .1
pigment { Orange } finish { ambient 1 }
}
cylinder { Red_Point2, Red_Point2 - <0,0,20>, .1
pigment { Red } finish { ambient 1 }
}
/* something to make the curve show up */
lathe {
bezier_spline
8,
Red_Point, Orange_Point, Green_Point, Blue_Point
Blue_Point, Green_Point2, Orange_Point2, Red_Point2
pigment { White }
finish { ambient 1 }
}
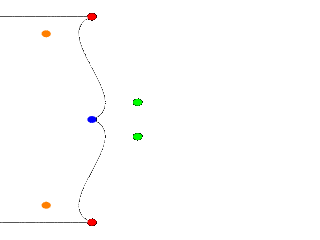
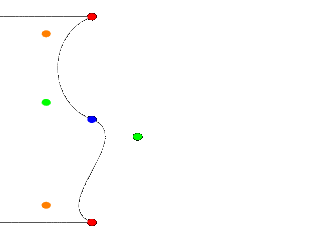
A nice curve, but what if we want a smooth curve? Let us have a look at the tangents on the Blue_point, draw the
lines Green_Point, Blue_point and Green_Point2, Blue_point. Look at the angle they make, it is as sharp as the dent in
the curve. What if we make the angle bigger? What if we make the angle 180°? Try a few positions for Green_point2 and
end with #declare Green_Point2 = <1.00, 4.50>;. A smooth curve. If we make sure that the two
control points and the connection point are on one line, the curve is perfectly smooth. In general this can be
achieved by #declare Green_Point2 = Blue_Point+(Blue_Point-Green_Point);
The concept of splines is a handy and necessary one, which will be seen again in the prism and polygon objects. But
with a little tinkering we can quickly get a feel for working with them.
|
 |






