|
A torus is a 4th order quartic polynomial shape that looks like a donut or inner tube. Because this
shape is so useful and quartics are difficult to define, POV-Ray lets you take a short-cut and define a torus by:
TORUS:
torus
{
Major, Minor
[TORUS_MODIFIER...]
}
TORUS_MODIFIER:
sturm | OBJECT_MODIFIER
Torus default values:
sturm : off
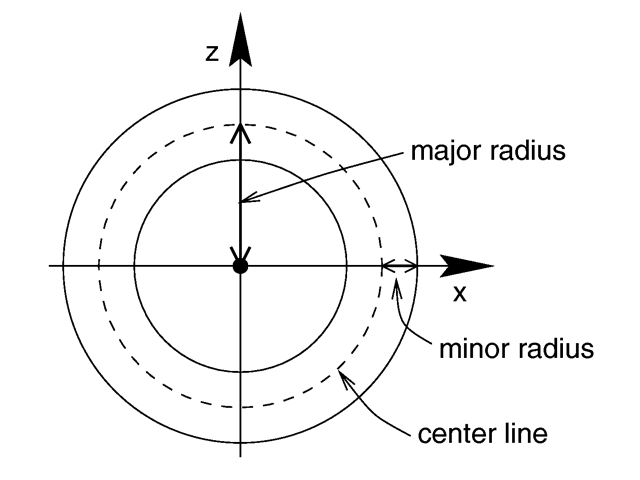
where Major is a float value giving the major radius and Minor is a
float specifying the minor radius. The major radius extends from the center of the hole to the mid-line of the rim
while the minor radius is the radius of the cross-section of the rim. The torus is centered at the origin and lies in
the x-z-plane with the y-axis sticking through the hole.
The torus is internally bounded by two cylinders and two rings forming a thick cylinder. With this bounding
cylinder the performance of the torus intersection test is vastly increased. The test for a valid torus intersection,
i.e. solving a 4th order polynomial, is only performed if the bounding cylinder is hit. Thus a lot of slow root
solving calculations are avoided.
Calculations for all higher order polynomials must be very accurate. If the torus
renders improperly you may add the keyword sturm to use POV-Ray's slower-yet-more-accurate Sturmian root
solver.
|






